标准差是数学和统计学中常用的一个概念,用于衡量一组数值的离散程度。简单来说,标准差表示数据点相对于平均值的偏离程度。标准差的计算公式基于方差,是方差的平方根。

标准差(Standard Deviation),通常用希腊字母σ(sigma)表示,计算公式如下:
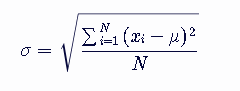
公式详解
σ 表示标准差。
N 表示数据点的总数。
xi表示每个数据点。
μ 表示所有数据点的平均值(算术平均数)。
注意:上述公式计算的是总体标准差。如果数据是样本数据,那么计算样本标准差时,分母应为 N−1 而不是 N,这是为了得到总体标准差的无偏估计。但在本案例中,我们假设数据是总体的,因此使用 N。
假设我们有以下一组数据:2,4,4,4,6。我们将使用这组数据来计算标准差。
步骤1:计算平均值(算术平均数)
首先,我们需要计算这组数据的平均值。平均值的计算公式是:
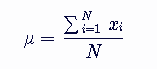
将数据代入公式:
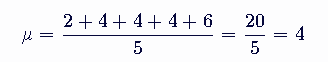
步骤2:计算每个数据点与平均值的差的平方
接下来,我们需要计算每个数据点与平均值之差的平方。这些差值分别是:
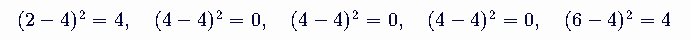
步骤3:计算方差
方差(Variance)是这些差的平方的平均值,计算公式为:
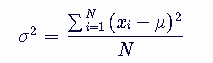
将数据代入公式:
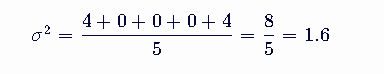
步骤4:计算标准差
最后,我们计算标准差,即方差的平方根:
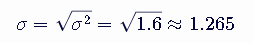
因此,这组数据的标准差约为 1.265。这表明数据点相对集中,因为标准差较小。标准差越大,表示数据点越分散;标准差越小,表示数据点越集中。
在标准差(或方差)的计算中,分母使用 N−1 而不是 N 的情况通常出现在我们处理的是样本数据,而不是整个总体数据的时候。这是为了校正偏差,使得样本方差(进而样本标准差)能够更准确地估计总体方差。
当我们从总体中抽取一个样本时,样本中的数值往往会比总体中的数值更接近样本均值,这是一种称为“样本均值偏差”的现象。如果我们使用 N 作为分母来计算样本方差,那么得到的方差通常会低于实际的总体方差,因为样本数据点相对于样本均值的偏离程度通常会比相对于总体均值的偏离程度要小。
为了补偿这种偏差,我们使用 N−1 作为分母来计算样本方差,这种做法被称为贝塞尔修正(Bessel's correction)。这样计算出来的样本方差是对总体方差的一个无偏估计,即如果我们从同一个总体中抽取多个样本,并分别计算它们的方差,那么这些样本方差的平均值将趋近于总体方差。
因此,当我们处理的是样本数据,并且希望用样本来估计总体特性时,我们使用 N−1 作为分母来计算方差和标准差。然而,如果我们处理的是整个总体数据,而不是样本,那么就应该使用 N 作为分母来计算总体方差和标准差。